My Ultimate Frisbee page
Lately I've been playing only at the Thursday game, so if you buy a disc using Venmo or Paypal, I'll bring it with me
on the next Thursday so you can pick it up. Or if you want to pay cash, just let me know that you are coming and I will bring
some discs with me.
Where I play:
- The Encinal game: MWF at 12:30pm (frisbee standard time). Often at Cubberly in Palo Alto
- The Eagle Park game: Thursday at 12:30pm. Often at Eagle Park in Mountain View
 Click on this photo to see a higher resolution picture.
Click on this photo to see a higher resolution picture.
Recently I created three custom disc designs for both groups. With these designs, I was attempting to appeal to the somewhat geeky nature of many of our players. I have received my order from Discraft for 25 discs with design 1 as well as 25 disks with design 2, so let me know if you would like to purchase either one of these discs. I'm selling them at my cost, which is $12.50 per disc.
If I sell out of this production run and it looks like there is sufficient demand, I will probably order more, possibly including the third design as well. You can make payments to me for the discs you pick up at the field in cash or with a Venmo or Paypal payment to me at
 or by scanning the Venmo or PayPal QR code at the bottom of this page.
or by scanning the Venmo or PayPal QR code at the bottom of this page.
Design 1: Parametric
 Click on this image to see the full resolution design file.
Click on this image to see the full resolution design file.
The red and blue curves are known as Archimedean spirals. The equations of these
curves are shown next to each curve using the same color as the curve itself. The
exponent of theta determines how fast the curve spirals outward. The path of the text characters
are placed along yet another Archimedean spiral.
The small light green curve in the middle is a member of a class of curves known as a Hypotrochoid.
You will be familiar with this type of curve if you have ever played with a Spirograph toy in your youth.
To create this particular example of a Hypotrochoid, imagine a disk with a radius of 3 units. Attached to the surface of this disk is a stick of length 5 units with one end at the disk's center and proceeding
along the disk's radius. We place a pen at the other end of the stick (which will be 2 units outside of the disk's circumference). Now, without slipping, we roll this disk inside another larger disk with a radius of 5 units. As we do this, the pen will trace out the figure you see in this disc design. You can watch a simulation of this process with the pen, stick, and 2 disks
here.
The equation for this particular Hypotrochoid in the complex plane is as follows:
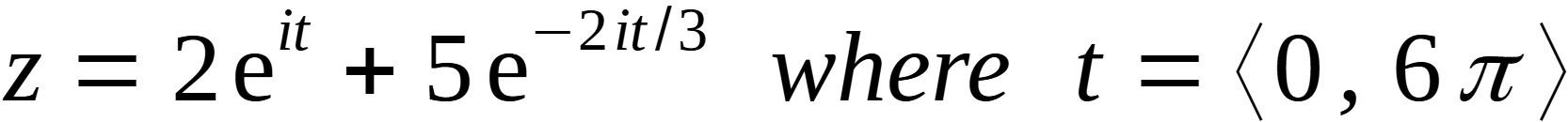
Design 2: 12 Circles
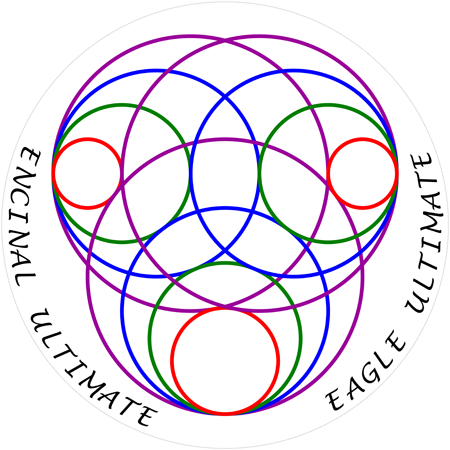
This disc design arose from the following not so well known geometrical puzzle:
Draw 12 circles in a plane so that every circle is tangent to exactly 5 others.
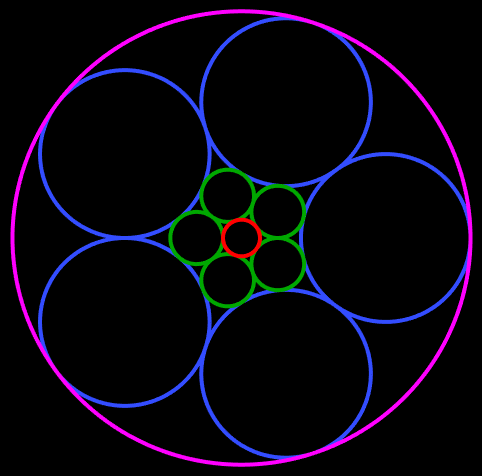 This is the solution provided by the puzzle's author.
I saw this solution before I saw the statement of the puzzle, so I don't know if I would have come up
with it or not, but my contribution to this solution was to derive these equations for the radii of the circles that ensures the desired tangencies:
(r1, r2, r3, r4
are the four radii from smallest to largest)
This is the solution provided by the puzzle's author.
I saw this solution before I saw the statement of the puzzle, so I don't know if I would have come up
with it or not, but my contribution to this solution was to derive these equations for the radii of the circles that ensures the desired tangencies:
(r1, r2, r3, r4
are the four radii from smallest to largest)
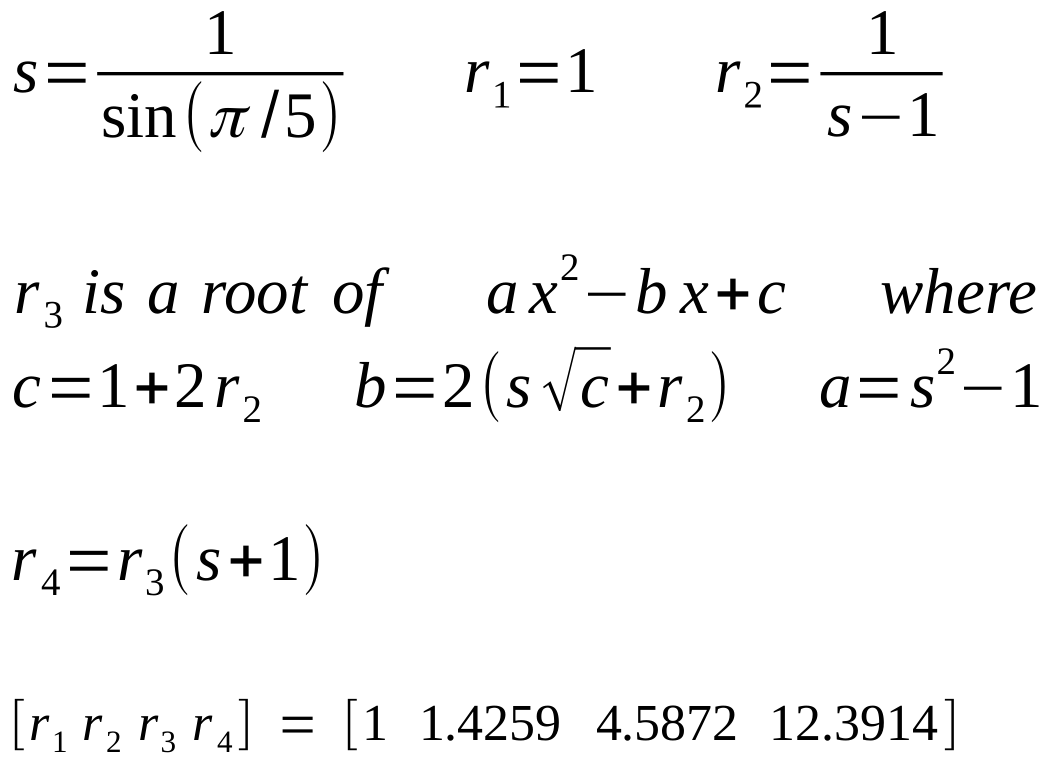
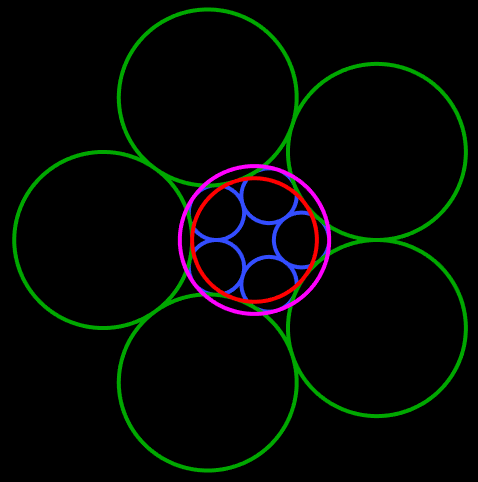 From this work, I realized that there are 3 variations of this solution, one if which is shown here.
I don't think it will take you long to see what the other two variants are. None of the variants seemed
to be as pleasing to the eye as the original solution, which I briefly considered using for the disc design.
From this work, I realized that there are 3 variations of this solution, one if which is shown here.
I don't think it will take you long to see what the other two variants are. None of the variants seemed
to be as pleasing to the eye as the original solution, which I briefly considered using for the disc design.
The fact that this puzzle has any solutions at all seemed somewhat remarkable to me, but I thought I would
try to find other solutions. And indeed I did find one, which is shown below.
 Click on this image to see the full resolution design file.
Click on this image to see the full resolution design file.
This is the solution of the puzzle that I chose for the disc design because it seemed to be the most
surprising. I don't know if there are any more solutions to this puzzle, but if you find one I would greatly appreciate you telling me about it. I found that the radii needed to make this solution
work are as follows:
Looking at the tangent point at the bottom where four circles meet, the radii of the red, green, blue, and purple circles are 17/11, 2.2, 3, 4 respectively.
Looking at the tangent point at the far right or far left where four circles meet, the radii of the
red, green, blue, and purple circles are 1, 2, 3, 4 respectively. The only requirement for that sequence
is that the middle two numbers have the same sum as the end two numbers, so for example 1, 3, 4, 6 would
have worked equally well although it might not be as pleasing to the eye.
For the 1, 2, 3, 4 sequence chosen here, notice that there are only 6 different circle sizes.
All 3 purple circles are the same size and all 3 blue circles are also the same size. Yet the red circles come
in two sizes as do the green circles. Surprising indeed!
Another interesting bonus with this design is that it looks somewhat like a face ... of an alien or perhaps a bug?
 After my disc designs came out, one of my fellow frisbee players said he came up with a family of solutions to
the 12 circle puzzle similar to my disc design except that it had 120 degree symmetry. His freehand sketch looked
something like the solution shown here (on the left side of the plot). The 3 smallest circles have radii of
1, 2, 3 (red,green,blue) although actually those sizes are completely arbitrary. A solution can be
built with any sequence, as long as all three numbers are different. The fourth circle size (purple) is determined
from the other three, and with this particular sequence (1, 2, 3) the fourth circle size turns out to be
approximately 4.11684397. After working out this new solution I discovered another solution (shown here on the
right side of the plot) that also has 120 degree symmetry. An interesting aspect of this final solution is that
only 3 different circle sizes are used. This gives us a way to make the original problem more difficult. In
addition to the requirement that each of the 12 circles must be tangent to 5 others, we can add the requirement
that no more than 3 different circle sizes are allowed. This final solution meets that requirement unlike all
the earlier solutions. The smallest circles (red and blue) have a radius of 1 and the largest circles (green) have
a radius of 5, although these two numbers are arbitrary. The size of the purple circles are determined from the
other two and with this choice (1,5) the purple circles turn out to have a radius of approximately 2.30930734142.
In the spirit of Paul Erdos, I'm offering a $25 prize (two discs) to the first person to provide an expression
for the exact value for the size of this purple circle. If it turns out this value is one of the roots of a
polynomial equation, I will accept the coefficients of the polynomial as a solution even if that doesn't provide
an exact value for the circle size. (A reasoning that the solution is correct must be provided.)
After my disc designs came out, one of my fellow frisbee players said he came up with a family of solutions to
the 12 circle puzzle similar to my disc design except that it had 120 degree symmetry. His freehand sketch looked
something like the solution shown here (on the left side of the plot). The 3 smallest circles have radii of
1, 2, 3 (red,green,blue) although actually those sizes are completely arbitrary. A solution can be
built with any sequence, as long as all three numbers are different. The fourth circle size (purple) is determined
from the other three, and with this particular sequence (1, 2, 3) the fourth circle size turns out to be
approximately 4.11684397. After working out this new solution I discovered another solution (shown here on the
right side of the plot) that also has 120 degree symmetry. An interesting aspect of this final solution is that
only 3 different circle sizes are used. This gives us a way to make the original problem more difficult. In
addition to the requirement that each of the 12 circles must be tangent to 5 others, we can add the requirement
that no more than 3 different circle sizes are allowed. This final solution meets that requirement unlike all
the earlier solutions. The smallest circles (red and blue) have a radius of 1 and the largest circles (green) have
a radius of 5, although these two numbers are arbitrary. The size of the purple circles are determined from the
other two and with this choice (1,5) the purple circles turn out to have a radius of approximately 2.30930734142.
In the spirit of Paul Erdos, I'm offering a $25 prize (two discs) to the first person to provide an expression
for the exact value for the size of this purple circle. If it turns out this value is one of the roots of a
polynomial equation, I will accept the coefficients of the polynomial as a solution even if that doesn't provide
an exact value for the circle size. (A reasoning that the solution is correct must be provided.)
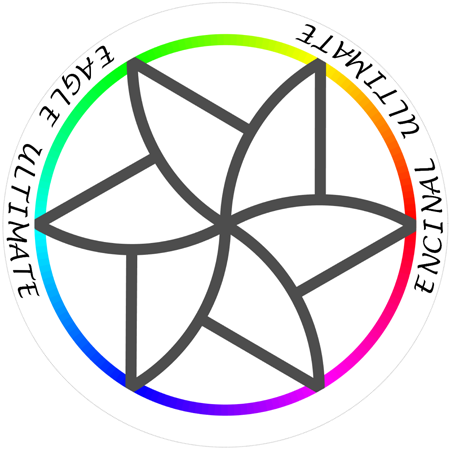
Design 3: Congruent Parts
This disc design arose from the following geometrical puzzle (also not so well known):
Divide a circle into n congruent parts so that at least one part does not touch the center.
 Click on this image to see the full resolution design file.
Click on this image to see the full resolution design file.
To solve the puzzle you may chose n to be any positive integer, although I am aware of only the
one solution shown here (with n=12). As before, if you discover other solutions to this puzzle,
I would love to know about it.
The multi-color circle is created with 180 segments with 180 different colors ... enough that the
color changes look continuous unless you zoom in to a small portion of the image.
And here is the Matlab code which I wrote to produce all three of these designs:
disc.m
After Matlab created the three figures, I printed them from the figure file menu directly
to a 600dpi png format using the Bullzip pdf printer which, despite its name, also allows
output to other graphics formats.
Below are some old pictures from the Encinal game (taken by Brent Gregory):
Scan codes for disc purchases:


 Click on this photo to see a higher resolution picture.
Click on this photo to see a higher resolution picture.
 Click on this image to see the full resolution design file.
Click on this image to see the full resolution design file.
 This is the solution provided by the puzzle's author.
I saw this solution before I saw the statement of the puzzle, so I don't know if I would have come up
with it or not, but my contribution to this solution was to derive these equations for the radii of the circles that ensures the desired tangencies:
(r1, r2, r3, r4
are the four radii from smallest to largest)
This is the solution provided by the puzzle's author.
I saw this solution before I saw the statement of the puzzle, so I don't know if I would have come up
with it or not, but my contribution to this solution was to derive these equations for the radii of the circles that ensures the desired tangencies:
(r1, r2, r3, r4
are the four radii from smallest to largest)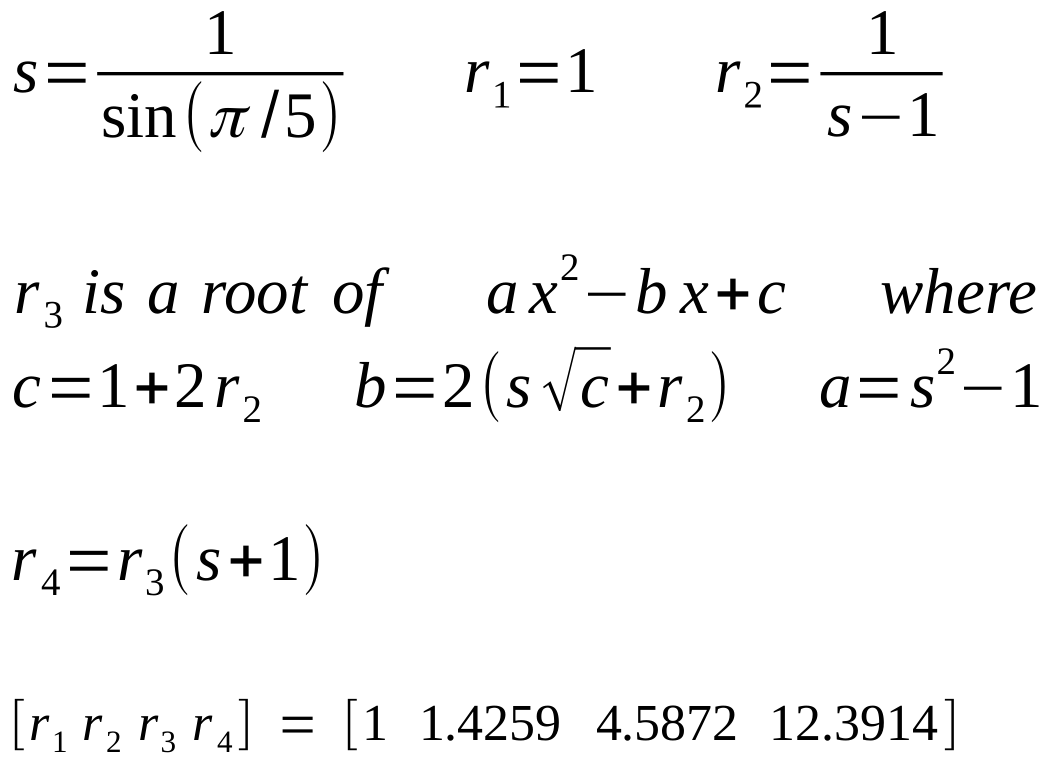
 From this work, I realized that there are 3 variations of this solution, one if which is shown here.
I don't think it will take you long to see what the other two variants are. None of the variants seemed
to be as pleasing to the eye as the original solution, which I briefly considered using for the disc design.
From this work, I realized that there are 3 variations of this solution, one if which is shown here.
I don't think it will take you long to see what the other two variants are. None of the variants seemed
to be as pleasing to the eye as the original solution, which I briefly considered using for the disc design.
 Click on this image to see the full resolution design file.
Click on this image to see the full resolution design file.
 After my disc designs came out, one of my fellow frisbee players said he came up with a family of solutions to
the 12 circle puzzle similar to my disc design except that it had 120 degree symmetry. His freehand sketch looked
something like the solution shown here (on the left side of the plot). The 3 smallest circles have radii of
1, 2, 3 (red,green,blue) although actually those sizes are completely arbitrary. A solution can be
built with any sequence, as long as all three numbers are different. The fourth circle size (purple) is determined
from the other three, and with this particular sequence (1, 2, 3) the fourth circle size turns out to be
approximately 4.11684397. After working out this new solution I discovered another solution (shown here on the
right side of the plot) that also has 120 degree symmetry. An interesting aspect of this final solution is that
only 3 different circle sizes are used. This gives us a way to make the original problem more difficult. In
addition to the requirement that each of the 12 circles must be tangent to 5 others, we can add the requirement
that no more than 3 different circle sizes are allowed. This final solution meets that requirement unlike all
the earlier solutions. The smallest circles (red and blue) have a radius of 1 and the largest circles (green) have
a radius of 5, although these two numbers are arbitrary. The size of the purple circles are determined from the
other two and with this choice (1,5) the purple circles turn out to have a radius of approximately 2.30930734142.
In the spirit of Paul Erdos, I'm offering a $25 prize (two discs) to the first person to provide an expression
for the exact value for the size of this purple circle. If it turns out this value is one of the roots of a
polynomial equation, I will accept the coefficients of the polynomial as a solution even if that doesn't provide
an exact value for the circle size. (A reasoning that the solution is correct must be provided.)
After my disc designs came out, one of my fellow frisbee players said he came up with a family of solutions to
the 12 circle puzzle similar to my disc design except that it had 120 degree symmetry. His freehand sketch looked
something like the solution shown here (on the left side of the plot). The 3 smallest circles have radii of
1, 2, 3 (red,green,blue) although actually those sizes are completely arbitrary. A solution can be
built with any sequence, as long as all three numbers are different. The fourth circle size (purple) is determined
from the other three, and with this particular sequence (1, 2, 3) the fourth circle size turns out to be
approximately 4.11684397. After working out this new solution I discovered another solution (shown here on the
right side of the plot) that also has 120 degree symmetry. An interesting aspect of this final solution is that
only 3 different circle sizes are used. This gives us a way to make the original problem more difficult. In
addition to the requirement that each of the 12 circles must be tangent to 5 others, we can add the requirement
that no more than 3 different circle sizes are allowed. This final solution meets that requirement unlike all
the earlier solutions. The smallest circles (red and blue) have a radius of 1 and the largest circles (green) have
a radius of 5, although these two numbers are arbitrary. The size of the purple circles are determined from the
other two and with this choice (1,5) the purple circles turn out to have a radius of approximately 2.30930734142.
In the spirit of Paul Erdos, I'm offering a $25 prize (two discs) to the first person to provide an expression
for the exact value for the size of this purple circle. If it turns out this value is one of the roots of a
polynomial equation, I will accept the coefficients of the polynomial as a solution even if that doesn't provide
an exact value for the circle size. (A reasoning that the solution is correct must be provided.)
 Click on this image to see the full resolution design file.
Click on this image to see the full resolution design file.

